Understanding how to set up a texture in JavaFX's TriangleMesh isn't hard. So much so, that there is no explanation in the Javadocs, although that may be a little too drastic for some.
It doesn't exactly help either if, in order to create the object, one must call functions where long arrays of indeces are passed as parameters and where these indices are a mix of the vertices of the mesh faces and those of the texture. Not to mention the indices are an indirection of the coordinates passed in an earlier step that one must keep track of.
It doesn't exactly help either if, in order to create the object, one must call functions where long arrays of indeces are passed as parameters and where these indices are a mix of the vertices of the mesh faces and those of the texture. Not to mention the indices are an indirection of the coordinates passed in an earlier step that one must keep track of.
At the very least, taking advantage of using a statically typed language to create wrapper classes for all this mess of numbers and indeces could not be considered overengineering by any reasonable person
Back to the subject, what we call texture here is the appearance of a surface that covers a triangular mesh. A mesh is a set of connected triangular faces in a three dimensional space where each of them has two sides: a front and a back. A mesh is modelled by the class TriangleMesh.
A MeshView object is an object with the mesh data plus some other non-spatial information, such as a "material". A MeshView is the actual object that will eventually be displayed on the screen.
How Setting the Texture in a TriangleMesh Works
For every face of the mesh (remember: a face is a set of three pairs of coordinates and the direction of its front side), the class allows the user to map each of its points, or vertices, to points in a two-dimensional space of side one size: a square of side one.
In other words, each spacial coordinate will be mapped to a point on a plane laying between (0, 0) and (1,1).
Naturally, the size of this space is completely arbitrary and, in fact, one may use whichever points in it they please and achieve the same result (we'll see this below). Furthermore, we can use the same point for all three vertices if we want, which can never be the case for the spatial coordinates, for obvious geometrical reasons. We'll also see this below.
The final step takes place in the MeshView object. When the Material object is set, the image file in that material, if there is one, can be viewed, conceptually, as if it were redimensioned to a square of side one and, for a given face, the texture points set earlier, will define the part of the image that covers it.
The following examples illustrate the explanation above. They also show how to work backwards from the specification of the problem to the implementation.
The following examples illustrate the explanation above. They also show how to work backwards from the specification of the problem to the implementation.
Example 1: Mesh With a Different Image On Each Side
In this example we have a 3D triangle mesh that is a solid. Specifically, a regular octahedron. An octahedron is a solid composed of eight equilatelar triangles.
Let's assume we want a different specific image -or pattern, or, as in this case, letter- on each side:
Let's assume we want a different specific image -or pattern, or, as in this case, letter- on each side:
Since the texture is defined on a plane, we can always start by spreading the mesh onto one.
The next step is calculating the coordinates of the faces. We start by fitting the shape in a square. It doesn't actually matter how. For simplicity, let's dock the shape to the left and bottom and then make the longer dimension of the shape, horizontal in this case, be of distance one.
We could have fitted the shape any other way if we wanted. It doesn't make a difference to the end result. Here's a whimsical example:
The final step is using an image for the material applied to the MeshView object.
What should that image look like? As you may have deduced already, it should be a square that matches precisely the same proportions as the diagram we used above to calculate the texture point coordinates, although the size of this square is irrelevant.
In other words, the shape should be located inside the canvas with the same relative position as in the diagram.
Let's see how all this translates to code:
TriangleMesh mesh = new TriangleMesh();
mesh.getPoints().addAll(
0f, 0f, 100f,
0f, 100f, 0f,
100f, 0f, 0f,
0f, -100f, 0f,
-100f, 0f, 0f,
0f, 0f, -100f);
mesh.getTexCoords().addAll(
0.571f, 0.27f,
0.143f, 0.508f,
0.429f, 0.508f,
0.714f, 0.508f,
1f, 0.508f,
0f, 0.7567f,
0.286f, 0.7567f,
0.571f, 0.7567f,
0.857f, 0.7567f,
0.429f, 1f);
mesh.getFaces().addAll(
0, 0, 3, 2, 2, 3,
0, 2, 2, 7, 1, 3,
0, 2, 4, 6, 3, 7,
0, 2, 1, 1, 4, 6,
1, 1, 2, 5, 5, 6,
2, 6, 3, 9, 5, 7,
3, 7, 4, 8, 5, 3,
4, 3, 1, 8, 5, 4);
1. In the first call, we set the octahedron coordinates. These are actual coordinates for an octahedron, in case you were wondering.
2. In the second, we set the plane coordinates for the texture. These are also the actual coordinates for the texture as in the diagram seen before.
3. In the final step we set the faces. Each of those numbers are indices that reference the order of the parameter passed on the previous calls. The indices on the even positions are the spatial coordinates, and the rest are the textures. So, for example, the first "0" references the first spatial point (0, 0, 100) passed in the first call. While the fourth number, "2", references the third texture point (0.429, 0.508).
The final step takes place in the MeshView object by setting up the image that covers the mesh.
Image image;
// initialize the Image
// ...
PhongMaterial material = new PhongMaterial();
material.setDiffuseMap(image);
TriangleMesh octahedronMesh = new TriangleMesh();
// initialize the mesh as above
// ...
MeshView octahedronView = new MeshView(octahedronMesh);
octahedronView.setMaterial(material);
Example 2: Mesh With a Different Color On Each Face
In this example we will see how to apply the texture coordinates in a less obvious way than before.
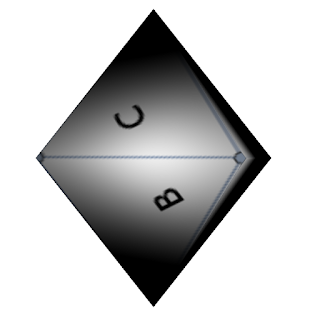
Let's say, we want this end result:
For the sake of simplicity, we will assume this is a mesh with only two faces: the ones visible in the image.
How would one go about creating the texture coordinates? Since we are interested in covering a face with one color, we only need one point per face, not three. Or to be more precise, we need to pass the same index three times in the getFaces().addAll() call.
For the texture let's use a square of side one split in two parts like this.
We only need one red point and one green point from it, which could be (0.2, 0.5) and (0.7, 05), for example.
In the code above we've highlighted the spatial coordinates in yellow and the texture coordinates in blue.
For the first face the texture is always point number 0, that is, (0.2, 0.5), which is a red point. Similarly for all vertices of the second face we indicate the index 1, which is the second texture coordinate that corresponds to a green point.
For this I created a small library that provides a facade for the creation of TriangleMesh objects.
There is some complexity we can simply not get rid of, as long as we are trying to represent visual information with code. If the mesh is small enough I would advice giving meaningful names to the vertices and faces, such as topPoint, or frontLeftFace. For larger meshes a better solution would be to store the coordinates in files that can be loaded at runtime.
Including links to diagrams in the comments or the project documentation is another good idea, if not very maintainable.
This library will be discussed in a separate post.
Let's say, we want this end result:
For the sake of simplicity, we will assume this is a mesh with only two faces: the ones visible in the image.
How would one go about creating the texture coordinates? Since we are interested in covering a face with one color, we only need one point per face, not three. Or to be more precise, we need to pass the same index three times in the getFaces().addAll() call.
For the texture let's use a square of side one split in two parts like this.
We only need one red point and one green point from it, which could be (0.2, 0.5) and (0.7, 05), for example.
TriangleMesh simpleMesh= new TriangleMesh();
simpleMesh.getPoints().addAll(
ax, ay, az,
bx, by, bz,
cx, cy, cz,
dx, dy, dz,
);
simpleMesh.getTexCoords().addAll(
0.2f, 0.5f,
0.7f, 0.5f
);
simpleMesh.getFaces().addAll(
0, 0, 1, 0, 2, 0,
2, 1, 1, 1, 3, 1
);
In the code above we've highlighted the spatial coordinates in yellow and the texture coordinates in blue.
For the first face the texture is always point number 0, that is, (0.2, 0.5), which is a red point. Similarly for all vertices of the second face we indicate the index 1, which is the second texture coordinate that corresponds to a green point.
Is There a More Elegant Way of Setting Up Mesh Objects?
While reading all this you were probably thinking of ways to reduce the complexity of setting up those long list of numbers in a reliable way and, also, how to make the code at least barely readable.For this I created a small library that provides a facade for the creation of TriangleMesh objects.
There is some complexity we can simply not get rid of, as long as we are trying to represent visual information with code. If the mesh is small enough I would advice giving meaningful names to the vertices and faces, such as topPoint, or frontLeftFace. For larger meshes a better solution would be to store the coordinates in files that can be loaded at runtime.
Including links to diagrams in the comments or the project documentation is another good idea, if not very maintainable.
This library will be discussed in a separate post.





Comments
Post a Comment